반응형
길이라는 특성 하나만으로 무게를 예측한다는 게 말이 안 된다는
지난 시간의 문제점을 해결하기 위해 선형 회귀를 사용해볼 것이다.

선형 회귀에서 선과 점의 오차율은 음수가 될 수도 있기 때문에
모든 손실(잔차) 값에는 제곱을 해준 뒤 더해서 MSE(평균 오차 제곱)를 구한다.
구한 mse가 좋은 건지 알 수 없다.
여러 가지 선을 비교를 해보지 않았기 때문이다.
비교하기 위해 사용하는 게 미분이다.
미분으로 기울기를 변경해가며 mse가 최소인 지점을 찾아야 한다.
이 값이 최소가 되는 회귀식을 찾는 것을 최소 제곱법이라고 하고
방법은 경사 하강법(미분)을 사용해야 한다.
이 선형 회귀 알고리즘이 최소 제곱법을 찾아주고
이때 내부적으로 경사 하강법 알고리즘을 사용하는 것이다.
from sklearn.linear_model import LinearRegression
# 객체 생성
lr = LinearRegression()
# 훈련
lr.fit(train_input, train_target)
# 예측
print(lr.predict([[50]]))
# 농어무게 = a(기울기) * 농어길이 + b(절편)
# y = 39.017 * x - 709.018 실제 50을 넣어보면 1241이 나온다
print(lr.coef_, lr.intercept_) # (기울기, 절편)
# 점으로 흩뿌릴 때 쓰는 그래프 (훈련 세트의 산점도)
plt.scatter(train_input, train_target)
# 선형 그래프 (15에서 50까지 1차 방정식 그래프)
plt.plot([15, 50], [15 * lr.coef_ + lr.intercept_, 50 * lr.coef_ + lr.intercept_])
# 50cm 농어 데이터
plt.scatter(50, 1241.8, marker="^")
plt.xlabel("length")
plt.ylabel("weight")
plt.show()
# 결정계수 확인
# -> 훈련 데이터 결정계수는 잘나왔는데 테스트 데이터 결정계수가 너무 안나왔음 0.90은 나와야지 비슷해야해
# 2번 문제점 때문 => 특성이 길이 하나라서 그런거야!!
# 너무 훈련 세트에 맞춰서 만들어졌다 : 과대적합으로 본다
print(lr.score(train_input, train_target))
print(lr.score(test_input, test_target))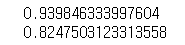
[출처]
머신러닝+딥러닝 » 혼자 공부하는 책
혼자 공부하는 머신러닝 딥러닝, 무료 동영상 강의, 머신러닝+딥러닝 용어집을 다운로드 하세요. 포기하지 마세요! 독학으로 충분히 하실 수 있습니다. ‘때론 혼자, 때론 같이’ 하며 힘이 되겠
hongong.hanbit.co.kr
반응형