선형 회귀를 사용하면 내가 예측한 값과 실제값의 잔차(+, -)가 발생한다.
그 라이브러리가 하는 일은 이 잔차들의 제곱의 총 합을 구해준다.
이게 SSE이다. 제곱 에러의 합!
이 SSE의 평균(= MSE)을 줄여나가는 과정을 최소 제곱법이라고 한다.
이 최소제곱법을 하기 위한 방법을 경사 하강법이라고 했다.
다항 회귀는 항을 늘려 가짜 데이터를 만드는 것이다.
항을 RDB로 치면 컬럼을 말한다.
더 이상 추가할 특성이 없을 때 다항 회귀를 사용한다.
만약 데이터가 [1, 2, 3] 3개 라면 머신러닝이 잘 학습하지 못한다.
데이터 양을 뻥튀기 해주기 위해 각각의 데이터에 제곱한 값을 추가한다.
[1, 2, 3, 1, 4, 9]
이렇게 제곱, 세제곱을 하여 데이터를 추가하는 것을 다항 회귀라고 한다.
더미 데이터가 생성되면 학습이 잘되어 결정계수가 높아지게 된다.
즉 독립 변인(길이) 하나로 종속 변인(무게)를 찾기 힘들 때,
샘플이 너무 적어서, 특성이 너무 적어서 찾기 힘들 때
더미 데이터(가짜 데이터)를 만든다.
# 더미 데이터 추가 (RDB로 치면 컬럼을 추가)
train_poly = np.column_stack((train_input ** 2, train_input))
test_poly = np.column_stack((test_input ** 2, test_input))
print(train_poly.shape)
print(test_poly.shape)
lr.fit(train_poly, train_target)
# 과소적합
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))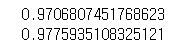
다항 회귀를 사용하여 데이터의 양을 늘려봤지만
테스트 세트의 점수가 더 높은 것으로 보아 과소 적합이 아직 남아있는 것 같다.
point = np.arange(15, 50)
plt.scatter(train_input, train_target)
# 21.6 (기울기 coef) 116.05 (절편값 intercept)
plt.plot(point, 1.01 * point ** 2 - 21.6 * point + 116.05)
plt.scatter(50, 1574, marker="^")
plt.show()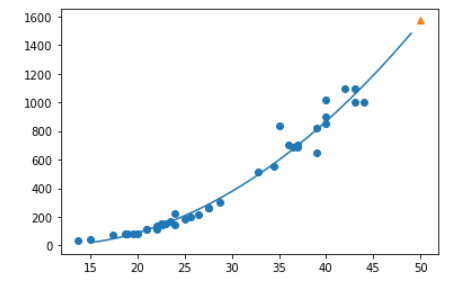
[출처]
머신러닝+딥러닝 » 혼자 공부하는 책
혼자 공부하는 머신러닝 딥러닝, 무료 동영상 강의, 머신러닝+딥러닝 용어집을 다운로드 하세요. 포기하지 마세요! 독학으로 충분히 하실 수 있습니다. ‘때론 혼자, 때론 같이’ 하며 힘이 되겠
hongong.hanbit.co.kr



